George Schils Business Blog - BZ Bread

This brief blog post gives the results of some random walk studies applied to the stock market. In particular, a segment of S&P 500 stock market data is used for the analysis. The question is how does the stock market data compare to a random walk. To answer this question, the power spectrum is computed for a segment of stock market data. It is known that the power spectrum of a random walk decreases as the square of the frequency. The analysis that we do computes the power spectrum of a section of S&P 500 data, and compares the fall off over frequency with that of a random walk.

I am using the terminology "ramdom walk" to mean Brownian motion, and I may be a bit sloppy in using this term. Even though I use the term "random walk" in this post, a better term would be "Brownian motion".

The first analysis that we do is for a time starting on January 1, 1950 and extending to January 1, 2013. The S&P 500 data over this period is used as input for the spectral analysis. The graphic below shows the result of the sample power spectrum, and also shows the ideal result for a pure random walk. The pure random walk has a power spectrum characteristic shown by the solid blue line. The sample power spectrum is shown as the jagged blue line. Because it is a sample spectrum, and not an average spectrum, one would expect it to be somewhat jittery, as we observe. It is observed that the sample power spectrum from the S&P 500 data closely follows the solid blue line for a pure random walk. Tentatively, this illustrates that the S&P 500 stock market data is very much that of a pure random walk. This is over the 63 year analysis period.

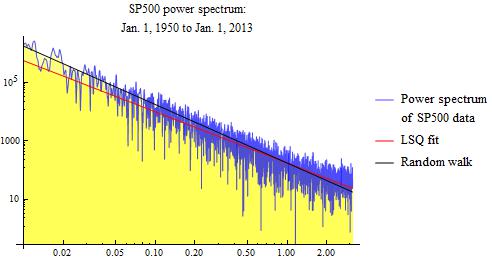
In the above log-log plot, the solid blue line has a slope of -2. This means that the spectrum falls off at a rate proportional to the square of the frequency. This is the power spectrum of an ideal random walk. It is seen to correspond closely to the sample spectrum for the S&P 500 data.

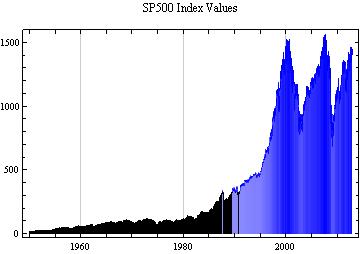
The actual data used in this analysis is given in the graphic below. This is the value of the S&P 500 index over the period of 63 years, extending from the year 1950 to the year 2013.

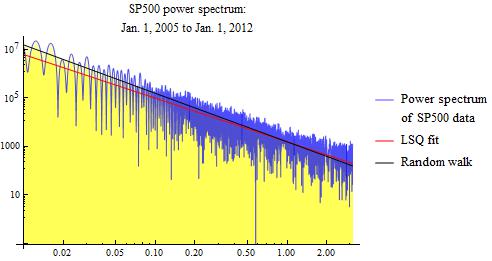
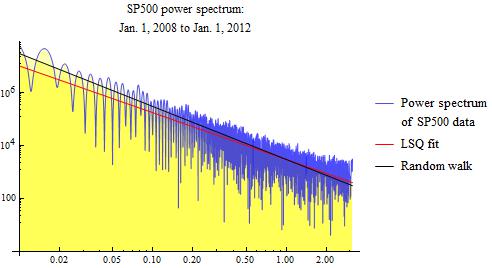
The basic result that stock market data follows a random walk appears not to depend strongly on the analysis period. We show results for two additional analysis periods. First, we look at data from 2005 to 2012. Secondly, we look at data from 2008 to 2012.

A random walk is a lot like a drunk staggering down the street. This article discusses some humorous aspects of this phenomenon.

The red line in the above power spectrum graphs is a least squares fit. This red line is a naive least squares fit, and can be subject to various errors. The slopes that I get for this least squares fit range from about -1.5 to -1.75, whereas pure Brownian motion has a value of -2. If these slopes are correct, it would indicate fractional Brownian motion.

The results discussed above are tentative. There are many technical issues that are beyond the scope of this article.

Related references: 1, 2, 3, 4.

Update 2

A plot of home prices using Case Shiller data is shown in the graphic below.

This plot is of the 10 city csxr index over a time period from about 1987. The right side of the graph shows that the home prices have been somewhat wobbling over the last several years. It's not great news; but it's also not bad news.

The short table below gives some numerical values. Column 1 is the year, column 2 is the 10 city csxr index value, and column 3 is the year to year (12 month) percentage increase.

2012.00 148.00  -4.12
2012.08 146.64  -3.77
2012.17 146.46  -2.95
2012.25 148.45  -2.19
2012.33 151.75  -1.03
2012.42 154.97  0.06
2012.50 157.24  0.58
2012.58 158.54  1.30
2012.67 158.87  2.09
2012.75 158.77  3.41

It is seen that the October 2012 csxr value of 159 is 3.41% higher than the value one year ago.

Case Shiller house price data for data up to June 2010 was just released. The numbers show nothing real surprising, and the basic trend of increasing home prices (compared to a year ago) appears to be continuing.

From June, 2009 to June, 2010, monthly home prices have increased 5.01%, whereas From May, 2009 to May, 2010, monthly home prices have increased 5.44%. (This latter number is slightly revised from a previous blog post.)

We have used the Case Shiller CSXR 10-city composite index in this analysis with non seasonally adjusted data.

The brief table below gives the 12-month home price percentage increases for the six months from January through June.

2010.00 -0.05
2010.08 1.46
2010.17 3.12
2010.25 4.60
2010.33 5.44
2010.42 5.01

In January home prices were still lower than they were a year ago, and since then they have shown increases compared to the same month of the previous year.

The year to year percentage increases are shown in the graph below.

There is a very slight downturn in home prices (i.e., in the home price increase rate - this can be very hard to understand), as seen at the very far right of the graph. It is probably too soon to know if this is a glitch or a real trend. The "glitch" at the right therefore shows a slight deceleration of home prices. Inspection of the graph shows that numerous "false glitches" do occur and the next few months will reveal whether this trend is real or a bump in the data. Of course the publishers of the index already know the answer since the data they release here is delayed by two months.

Case Shiller house price data for data up to May 2010 was just released. The numbers show nothing surprising, and the past trend of once again increasing home prices appears to be continuing nicely. House prices have increased compared to their prices a year ago.

From May, 2009 to May, 2010, monthly home prices have increased 5.40%, whereas From April, 2009 to April, 2010, monthly home prices have increased 4.63%. (This latter number is slightly revised from a previous blog post.)

The 12 month percentage gains appear to be increasing since the number for last month (March) was 3.14%.

We have used the Case Shiller CSXR 10-city composite index in this analysis with non seasonally adjusted data.

The brief table below gives the 12-month home price percentage increases.

January 2010    -0.05
February 2010   1.45
March 2010      3.14
April 2010      4.63
May 2010        5.40

In January home prices were still lower than they were a year ago, and since then they have shown increases compared to the same month of the previous year.

The graph below shows the percentage increases in home prices from year to year. That is, this is a 12 month price percentage change.

From April, 2009 to April, 2010, home prices have increased 4.61%. This is the right most point in the graph above. The 12 month percentage gains appear to be increasing since the number for last month (March) was 3.14%. We have used the Case Shiller CSXR 10-city composite index in this analysis with non seasonally adjusted data.

Case Shiller had stopped publishing its data in spreadsheet format. Or at least I was not able to locate their data in this format. I recently noticed that their data seems to be available in spread sheet format again, so I have resumed doing house price analysis. The analysis here is very similar to what I have been doing in the past but the data has been updated.

The graph below shows the percentage increases in home prices from year to year. That is, this is a 12 month price percentage change.

From March, 2009 to March, 2010, home prices have increased 3.15%. This is the right most point in the graph above. We have used the Case Shiller CSXR 10-city composite index in this analysis.

Case Shiller has stopped publishing its data in spreadsheet format. This means that I am going to stop publishing the kinds of studies that I have been doing in the past.

If I can locate spreadsheet data, I may continue to do this analysis in the future.

Case Shiller housing data is found at this link.

Analysis of cpi from data released on December 16, 2009 shows that the cpi increased by 0.1% from October to November. The cpi is higher by 1.8% from the same month (November 2008) a year ago. The data is given below. For the first time since February, the cpi is higher compared to the same month a year ago.

12 month percent change

May     Jun     Jul     Aug    Sep    Oct    Nov
-1.28   -1.43   -2.10   -1.48  -1.29  -0.18  1.84

1 month percent change

May     Jun     Jul     Aug    Sep    Oct    Nov
0.289   0.859   -0.159  0.224  0.062  0.096  0.071

Data is from the Bureau of Labor Statistics, and series CUUR0000AA0 is used. Data here is normalized so that 1967=100.

Home prices increased by 1.65% from June 2009 to July 2009, according to recent Case Shiller data.

The table below shows detailed data for the last seven months. The second column is the increase percentage for the same month one year ago. Column 4 is the monthly percentage increase. A new calculation is column 3, which is a kind of second derivative of the CSXR value - this is the home price acceleration. This is calculated as the difference between the yearly home price increases: the July 2009 acceleration is calculated as -15.07 - -12.77 = 2.30. In other words, the numbers for the year to year increases although still negative are increasing at an increasing rate.

January 2009    -19.44  -0.21   -2.55
February 2009   -18.88  0.55    -2.12
March 2009      -18.62  0.26    -2.04
April 2009      -17.96  0.66    -0.68
May 2009        -16.76  1.20    0.47
June 2009       -15.07  1.69    1.45
July 2009       -12.77  2.30    1.65

These numbers are for the CSXR 10-city index. Most media reports are for the 20-city index, so the results here are an interesting companion to other popular media reports.

From column 3 it is clear that home prices have accelerated for six months straight, and the acceleration is increasing.

Home prices are still lower than they were a year ago (by 12.8%) but at the same time home prices are accelerating.

Analysis of cpi from data released on September 16, 2009 shows that the cpi increased by 0.2% from July to August, but that the cpi is lower by 1.5% from the same month (August 2008) a year ago. The data is given below.

12 month percent change

Year Jan Feb Mar  Apr  May  Jun  Jul  Aug
2009 0.0 0.2 -0.4 -0.7 -1.3 -1.4 -2.1 -1.5 

1 month percent change

Year Jan Feb Mar Apr May Jun Jul  Aug 
2009 0.4 0.5 0.2 0.2 0.3 0.9 -0.2 0.2 

Data is from the Bureau of Labor Statistics, and series CUUR0000AA0 is used. Data here is normalized so that 1967=100.