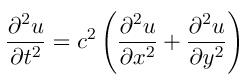
<< PDE page | math home | home
by George F. Schils
(Much of this work was done when George Schils worked on applied math research at FEREGO.)
This web page contains some sample analytic and numeric solutions to the one-dimensional wave equation. Some general theory is summarized and some solutions to specific problems are given.
The page builds on previous work on the two dimensional wave equation. In a sense the one dimensional equation is simpler and this allows one to focus on the analysis rather than on the details of computing.
Here is a sample solution of solving the wave equation in two dimensions with dependency on time.
Formally the scalar wave equation in two dimensions and in rectangular coordinates is given by
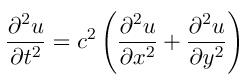
where c is the speed of light.
Here we focus on the simpler wave equation in one dimension, which is
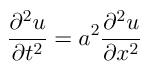 .
.
Here we have used a in place of c. This equation describes a vibrating string for example. Here a is the speed of the wave; a depends on the physical parameters of the problem.
u depends on x and t and is written as u = u(x,t). On this page we consider the boundary condition u(0,t) = u(1,t) = 0 and the initial condition u(x,t)=f(x). Here f(x) is the initial condition at t=0.
This problem is solvable analytically using techniques from Fourier analysis. Using the Fourier coefficients of the initial condition f(x)
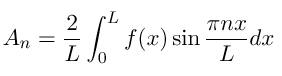
the closed form solution for u(x,t) satisfying the initial condition and the boundary condition is the Fourier series
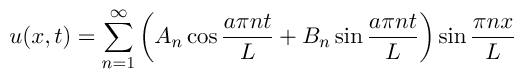 .
.
Here we are considering a special case in which Bn=0, which reflects the specification on the initial derivative.
This is an amazingly elegant solution. Trigonometric functions, sin and cos, describe the solution to this problem. Of course there is an infinite sum of such terms.
The solutions on this page are obtained by numerically evaluating the An coefficients and then performing the above Fourier sum numerically. Thus these techniques consist of numerically evaluating an analytic solution.
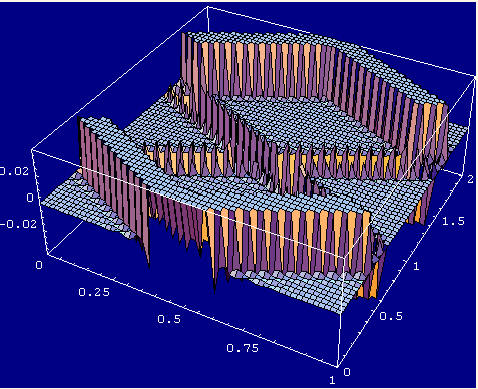
We next show a solution where the initial condition is a square pulse from x=0.4 to x=0.6. This is a pulse of unit height and width 0.1 that is centered around 0.5. When we solve the one-dimensional wave equation using this initial condition, we obtain the interesting plot shown below. This wave propagates on forever and repeats every 2 units of time. At t=2 it is seen that the same shape is obtained as for the initial condition t=0. The boundary conditions are that u(0,t) = u(1,t) = 0, that is, the wave is zero at the boundary determined by x=0 and x=1.
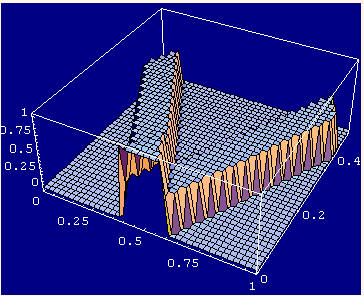
The plot gives detail over the time period from t=0 to t=0.5. During the time the pulse is seen to spread out.
Work for a Gaussian initial condition has been done and a web page write up is being prepared.
<< PDE page | math home | home
Web pages created by George Schils. Copyright © 2004-2005 George Schils. All rights reserved.