PDE solutions for the wave equation

by George F. Schils

(Much of this work was done when George Schils worked on applied math research at FEREGO.)

This web page contains some sample solutions to some partial differential equations of physics. We focus on the wave equation on this page.

Numerous analytic means exist for solving such equations. A very large body of literature has evolved for a period longer than a century regarding the solutions of this kind of problem. Many kinds of digital computer techniques also exist for solving partial differential equations. So we can only manage to just touch the tip of the iceberg regarding this very large area.

Advances in computing technology are allowing many more kinds of problems to be solved, and we can think about solving problems in higher dimensions as well. This web page contains some numerical solutions to two-dimensional partial differential equations, and this was unheard of - even on the fastest computers - just a few years ago. These calculations were even done on a relatively old Pentium machine.

Sturm Liousville

It is amazing how little there is on the internet regarding Sturm Liousville theory. We performed a search and found around 11 items mentioned on the internet.

Our expertise and interest is perhaps more in the analytical solution of such differential equations, many of which fall into the area of Sturm Liousville theory. Solving pde's as shown on this page involves many sophisticated techniques from mathematics, and one needs to draw from a reasonable set of inter-disciplinary tools. For example, one typically needs to be adept at dealing with special functions such as Fourier series or Fourier-Bessel series.

A disadvantage of finding analytical (closed form) solutions is that solutions only exist for very special cases. For example the equations must be linear, the boundary conditions need to be right, and only a relatively small set of coordinate systems exist. In contrast, digital solutions can find answers to much more non-ideal problems.

This web page begins a set of explorations of some pde's in which the solutions are numerical. At other places in our web pages we plan on discussing analytic solutions.

Wave Equation

Here is a sample solution of solving the wave equation in two dimensions with dependency on time.

Formally the scalar wave equation in two dimensions and in rectangular coordinates is given by

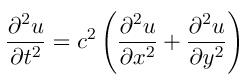
where c is the speed of light. For an equation which is so simple in form, an amazing set of work has evolved regarding its solution. The above equation appears simple; it is not though.

This equations is very similar to the equation for a vibrating drum or membrane in two dimensions. This web page's main purpose is the discussion of some solutions of pde's and although optics is interesting, the discussion of optics itself is not the main concern here.

Old reference. The book shown below is a classic in the field of electromagnetics. (It is in our reference library.) It was published around 1870, and sparked the beginning of the electric millennium.

In the examples on this page we normalize space (choose units) so that c = 1.

In solving the wave equation given above we are dealing with the so-called free space propagation of light. This is how light behaves in the absence of materials. Another common problem, not discussed here, is that of describing light as it passes through an aperture (or otherwise interacts with a boundary). This latter problem is quite different and a different set of solution techniques are used.

Solutions for different initial conditions

We illustrate a numerical solution of the wave equation in the case of several different initial conditions. The first example is for a Gaussian beam. Here the initial condition is a Gaussian shape. Very much is known about the propagation characteristics of Gaussian beams.

Generally it is convenient to choose functions which are eigen-solutions in the given coordinate system. Gaussian and Bessel beams often are convenient choices when dealing in radial (cylindrical) coordinate systems. A general Bessel-Gauss beam is given by

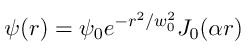Here w₀ is the beam "waist". A Gaussian beam can be taken as the special case where alpha = 0.

The analytical theory of the propagation of such beams can get very involved (even with appropriate simplifications of the wave equation). Analytic solutions using the above equation involve infinite series involving trigonometric functions, Bessel functions, and hyper geometric functions.

We have done some other simulation work (not discussed here) on the propagation characteristics of various Bessel-Gauss beams. (Some of this work may be brought out in other future discussions.)

The initial condition at t = 0 is that u(0,x,y) = exp[-(x^2+y^2)]. This Gaussian shape is seen in the first plot. Then as time proceeds, the Gaussian wave "spreads out" over space (x-y), and this is observed in the series of plots shown below. This is very much like a drop of water falling into a pond, and then watching the waves ripple out. The time is plotted from times 0 to 10. This is an interesting solution.

We also show a solution in which the initial condition is an elliptical Gaussian shape. This is not contained in the above formula for the Bessel-Gauss beam. The propagation characteristic in this case is also interesting to observe.

We next show a solution where the initial condition is more "squarish". Indeed, this initial distribution is the function 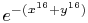. Many of the characteristics of super Gaussian wave forms are known, but this result has sparked a further interest on our part. It is interesting that this more rounded initial condition results in a narrower pulse (sharper) propagation characteristic. That is, a smoother input initial condition results in a sharper propagation characteristic. (We are not sure this is a valid general or specific conclusion.) We are attempting to further understand this behavior from an analytical viewpoint.

More work is being done and more simulations are being done. Analytic solutions along with additional simulations are being prepared for some of the examples presented above.

<< PDE page | math home | home