PDE Solutions of 1D wave equation

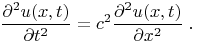
by George Schils

at FEREGO Math Research

This page demonstrates some solutions of various pde's of mathematics and physics.

We present a solution of the one-dimensional wave equation

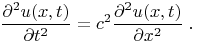
This equation would describe a vibrating string (such as a guitar string) or a wave traveling in a one-dimensional waveguide, for example.

Pulse initial condition. The initial conditions on t and the boundary conditions on x are given as

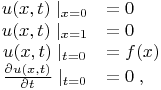
where the initial condition function 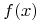is a pulse.

The graphic presented below is an accurate numerical calculation of a closed form analytic solution of the above pde. The analytic solution is obtained using Sturm Liousville techniques. (In Russian these are called Steklov techniques). The boundary conditions are that the solution is zero at x=0 and x=1. The initial shape at t=0 is a square pulse.

This solution is more difficult numerically because of the "sharp corners" present.

It is seen that the sharp corners stay sharp. This is an interesting propagation characteristic. In a sense this could be said to be an example of square propagation.

Normal initial condition. The same equation is solved again using the initial condition function 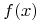equal to the Gaussian shown below.

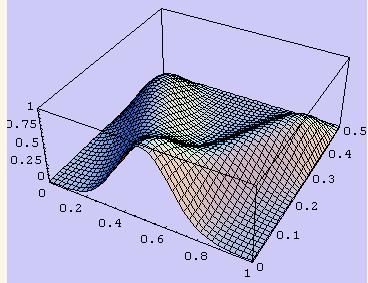
Again a full Sturm Liousville solution is obtained and is plotted below for time t in [0, 0.5].

The solution over a longer time period is also obtained and is shown below.

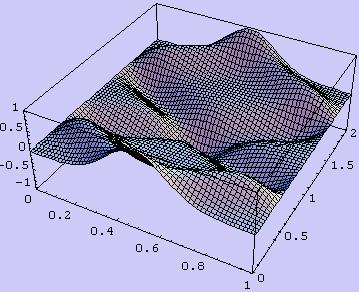
This solution is kinder numerically because there are no sharp corners present.

The propagation characteristics for this normal (gaussian) initial condition are also interesting.

<< math home | home