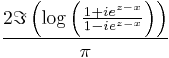
by George Schils
(Some of this work was done when George Schils worked on applied math research at FEREGO.)
Around 2004 George Schils began doing some basic explorations of harmonic functions. This was in association with additional learning in the area of complex variable theory. Numerous practice problems were performed and some theoretical and computational studies have been performed. This page includes a few items from that work. This work is done for learning, to practice computational examples, sometimes to develop or test computer codes, and in general to increase the set of tools that can be used to solve problems.
Harmonic functions are functions that satisfy Laplace's equation in two dimensions. This represents a very important class of functions, for harmonic functions play a role in the solution of many classical problems in physics and engineering. Generally harmonic functions might be expected to play a role in cases where one is concerned with the equilibrium solution of either wave-like or diffusion-like equations in two dimensions. In addition to solving many equilibrium problems in two dimensions related to electromagnetics and heat transfer, harmonic functions might also play a role in societal and money systems to give a few examples.
Harmonic functions are related to analytic functions in complex variable theory in that both the real part and the imaginary part of an analytic function, by virtue of the Cauchy Riemann equations, also satisfy Laplace's equation, and are therefore harmonic functions. Thus the powerful machinery of complex variable theory can be brought to bear in solving many diverse problems in physics, engineering, and elsewhere.
As long as a function is analytic, it is therefore harmonic. This means that a large set of powerful methods from conformal mapping theory can be applied to solve Laplace's equation in two dimensions.
What this basically means is that you can take any analytic function and bend it around to meet the boundary conditions. After the bending, it is still a harmonic function. As such, this represents an extremely powerful solution method for two dimensional Laplacian equation problems.
We give a textbook example from example 2 on p. 233 of Analytic Functions by M. A. Evgrafov, Dover, 1966.
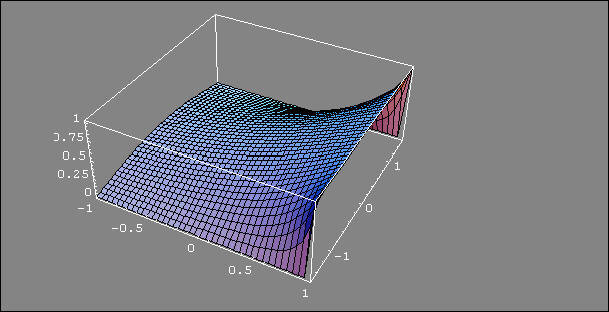
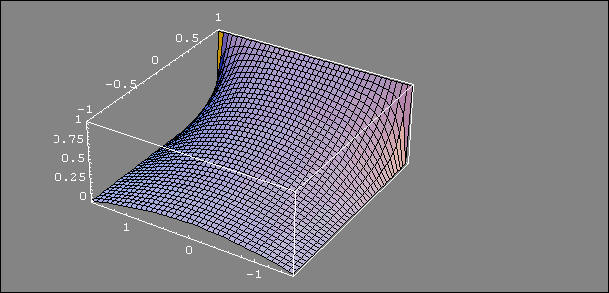
Solve Laplace's equation for the problem where the function is unity for x=1 and y between -pi/2 and pi/2 and that is zero along the lines y= -pi/2 and y=pi/2. As argued at the given reference, the analytic function,
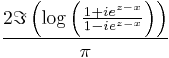
where we use x=1, solves this problem. It is plotted below in two different views.
Web pages created by George Schils. Copyright © 2005 George Schils. All rights reserved.