Integer properties of $\lambda_1^n$

It is clear that $x(n)$ is always an integer for all $n$. A simple manipulation of Eq. 16 gives

$$\left( {1 + \sqrt{5} \over 2} \right) ^{n} = x(n-1) - \left( {1 - \sqrt{5} \over 2} \right) ^{n} \; . \eqno(17)$$

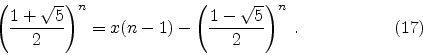
The second term on the right hand side of this equation becomes exponentially small as $n$ increases, and the first term on the right hand side is always an integer. Thus the left hand side of Eq. 17 exponentially approaches an exact integer as $n$ increases.

For example, the $149^{th}$ Bob integer is $22291846172619859445381409012498$ and the numerically calculated value of $\lambda_1^{150}$ is

  22291846172619859445381409012497.999999999999999999999999999999955140548