Specific Solution

Our interest in this paper is to solve the system equations 6 and 7 for the specific matrix given by Eq. 5.

We can verify by direct multiplication the relation

$${1 \over \sqrt{5}} \left[ \begin{array}{cc} 1 & 1 \\ - {... ...rray}{cc} 1 & 1 \\ 1 & 0 \end{array}\right] \; , \eqno(12)$$

and so comparing to Eq. 9

$$\lambda_1 = {1-\sqrt{5} \over 2} \eqno(13)$$

$$\psi = \lambda_2 = {1+\sqrt{5} \over 2} \eqno(14)$$

and

$$S = \left[ \begin{array}{cc} 1 & 1 \\ - {{\sqrt{5}+1} \... ... 2} & {\sqrt{5}-1} \over 2 \end{array}\right] \; . \eqno(15)$$

It is clear that $\lambda_1 \lambda_2 = -1$, so the $\lambda$'s are negative reciprocals. The number $\psi$ is called the golden ratio.

Multiplying out Eq. 11, making substitutions from Eqs. 13-15, performing some algebra, and taking the second element of the vector gives the desired representation for the $n^{th}$ Bob integer

$$x(n) = \left( {1 + \sqrt{5} \over 2} \right) ^{n+1} + \left( {1 - \sqrt{5} \over 2} \right) ^{n+1} \; . \eqno(16)$$

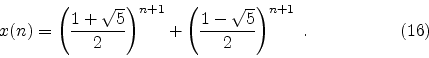
This is a remarkable result!