Ramanujan fractions and identities

We have begun to do some research regarding some results of Ramanujan called his ``third notebook'' results.² There are results which apparently were not known to Ramanujan. These are interesting and deep results. The work below is based on the results of Rajesh Ram and on results published in his web pages.

Define the functions $P(m)$, $Q(m)$, $R(m)$, and $S(m)$ for complex $a$, $b$, and $m$ as:

$$\begin{array}{cl} P(m) =& (11a + 6b)^m + (-5a - 11b)^m + (-... ...S(m) =& (-9a + b)^m + (-a - 10b)^m + (10a + 9b)^m . \end{array}$$

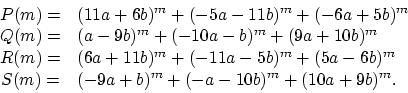
The dependence on $a$ and $b$ has not been shown.

A number of amazing results regarding the above definitions are found to exist.