Generalized Fibonacci Number Representations

There are at least two somewhat extant papers on some representations of generalized Fibonacci numbers, exact integers, and related spaces. These were written by a FEREGO researcher under collaboration with Robert Bastaz.¹ These papers are lost and missing.

The results lost in these papers have been recreated, and summary results are presented at the http://www.FEREGO.com site.

Both the results themselves as well as the techniques used for their derivation are interesting.

One very interesting result from this work is the representation of the $n^{th}$ number in the sequence 1, 3, 4, 7, 11, ... as

$$x(n) = \left( {1 + \sqrt{5} \over 2} \right) ^{n+1} + \left( {1 - \sqrt{5} \over 2} \right) ^{n+1} \; .$$

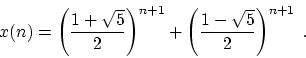
Defining the ``golden ratio'' number $\psi = {1 + \sqrt{5} \over 2}$, this assumes the simpler form

$$x(n) = \psi ^{n+1} + \left( - \psi \right) ^{-(n+1)} \; .$$

This is an amazing and extremely elegant result.

It is also easy to argue that powers of the ``golden ratio'' $\psi$

$$\psi^n = \left( {1 + \sqrt{5} \over 2} \right) ^{n}$$

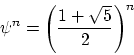
approaches an exact integer as $n$ gets large.

Generalizations of these results have also been obtained.