 .
.
We have recently done some work regarding Sterling's formula.
Sterling's formula is an approximation to the factorial function and is given by the formula
 .
.
This formula is useful for many kinds of approximations involved in combinatorial analysis. For example, this approximation is used often in performing complexity calculations regarding computer programs. Entropies and other combinatorial quantities can be approximated by this formula when asymptotic complexities for large "n" are required.
Although Sterling's formula is often cited in books, finding a proof of the result is more difficult. We have studied such a proof to understand the source of the formula. This understanding has allowed us to derive some additional terms in the Sterling formula approximation, thus allowing more accurate asymptotic approximations to be done.


This formula is stunningly accurate. We give some comparisons between the exact result and the above very accurate approximation.
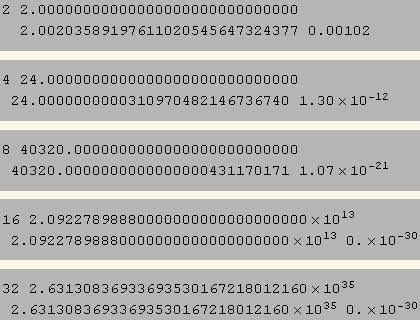
Accuracy comparison using more accurate
Sterling's formula.
Copyright @ 2005 FEREGO. All rights reserved.