Mikusinski Notes
by George Schils
This page discusses some elements of operational calculus found in the book
Operational Calculus, Lectures given by A. Erdelyi, Mathematics Department, California Institute of Technology, Pasadena, 1955.
|
It is not in final form, and there may be errors.
Mikusinski notes.
This page is under development.
1. Exponential
functions
2. Laplace
transformation
3. Bessel function
results
4. Error function
results
In Mikusinski operational calculus, results appear to the the
same as with Laplace transforms. However, the meanings of the
equations are very different. For example, in the equation below
the variable  is not a complex
variable as with Laplace transforms, but is the operational
function
is not a complex
variable as with Laplace transforms, but is the operational
function  , which is the
inverse of integration, and which is roughly equivalent to the
operation of differentiation.
, which is the
inverse of integration, and which is roughly equivalent to the
operation of differentiation.

What this means more precisely is that when both sides are
multiplied by  the identity
function results. This identity function is not the function which
is one everywhere, but is the generalized-function identity
function, or the delta function.
the identity
function results. This identity function is not the function which
is one everywhere, but is the generalized-function identity
function, or the delta function.

Multiplication here means convolution: it is not ordinary multiplication.
To further understand the above result, we now note the derivative theorem.

This form is the same as with Laplace transforms. It says to
differentiate a function  , one
convolves with the differentiation operator
, one
convolves with the differentiation operator 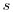 and then subtracts the initial value.
Alternatively multiplying by
and then subtracts the initial value.
Alternatively multiplying by  is equivalent to differentiating and adding the initial value:
is equivalent to differentiating and adding the initial value:

Performing this operation on the equation after Eq. (1) then gives
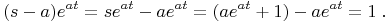
This is not a proof, but we have performed a few simple manipulations to show the plausibility of the result in Eq. (1).
It is shown that the exponential function has a reasonable
interpretation for reasonable functions. That is, if 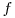 is an integrable function, then
is an integrable function, then

Here  refers to the
refers to the
 convolution of the function
convolution of the function
 with itself, and
with itself, and 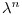 is the ordinary
is the ordinary 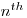 power of the number
power of the number  .
.
The entity  does not have
an expansion as above, which makes sense since
does not have
an expansion as above, which makes sense since  is not an integrable function. What
holds, instead is the identity
is not an integrable function. What
holds, instead is the identity

This relation holds for any integrable function 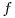 , no matter what the growth rate of
, no matter what the growth rate of
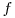 is. This is a Laplace
transform like relation which holds true regardless of the growth
rate of
is. This is a Laplace
transform like relation which holds true regardless of the growth
rate of  . This essentially
says that a function
. This essentially
says that a function  is the
Laplace transform of itself. In Mikusinski operational calculus
there are no two domains as there are in ordinary Laplace
transforms.
is the
Laplace transform of itself. In Mikusinski operational calculus
there are no two domains as there are in ordinary Laplace
transforms.
To see how Eq. (1) is a Laplace transform relation, we proceed
as follows. Using equation (4) with the function 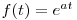 , and also using Eq. (1), we
obtain
, and also using Eq. (1), we
obtain
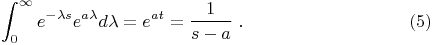
The first and third elements of this equation give the more familiar form of the Laplace transform. We again note that the variable s here is not a complex variable as in Laplace analysis, but instead is the name for a certain generalized function which is a kind of differential operator. Thus there is an exact similarity between Laplace transforms and Mikusinski operational calculus. This allows tables of Laplace transforms to be used in this kind of operational calculus.
The s operator was seen above to be an interesting generalized function. It is very close to the differentiation operator.
Now we present some results for Bessel functions. These involve
even more obscure functions of 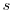 .
.

and
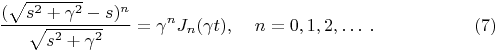
Doing a manipulation similar to that in Eq. (5), we see that the Laplace transforms of the right hand sides of the above two equations gives the left hand sides. This is the more familiar Laplace transform interpretation.
Some even more obscure results are derived.
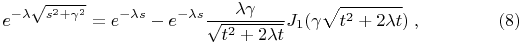
and

Eqs. (8) and (9) can be rearranged so that  appears on one side and
appears on one side and  on the other side. Doing so gives
appropriate Laplace transform relationships. (We leave this as an
exercise for the reader.)
on the other side. Doing so gives
appropriate Laplace transform relationships. (We leave this as an
exercise for the reader.)
This section will contain results on the error function
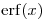 , and on related
functions.
, and on related
functions.
