Basic Future Value Equations

Let us start with the simplest compounding situation in which there is an amount of money $M$ which grows at a the per unit interest rate $i$. The differential equation for the balance of money $x(t)$ at time $t$ is

$${ dx(t) \over dt } = i x(t)$$

It is simple to verify by direct substitution that the solution

$$x(t) = M e^{it}$$

satisfies this differential equation along with the initial condition $x(0) = M$. This is the basic formula for the continuous compounding of a deposited amount of money.

Let us start with a problem of the compounding of money. Assume at the start we have zero money and a constant stream if income denoted by $u(t)$. If the interest rate is $i$ then the continuous accumulation or compounding of money satisfies the differential equation

$${ dx(t) \over dt } = i x(t) + u(t) .$$

The solution of this equation is found for a general deposit rate $u(t)$ to be

$$x(t) = \int_0^t e^{i (t-\tau)} u(\tau) d\tau = \int_0^t e^{i \tau} u(t-\tau) d\tau .$$

It can be verified by differentiation and direct substitution that this satisfies the above differential equation.

If the amount of money at time $t=0$ is $M$ then the solution is given by

$$x(t) = M e^{it} + \int_0^t e^{i (t-\tau)} u(\tau) d\tau .$$

and the previous result is seen as a special case with $M=0$.

An important special case occurs when the deposited money $u(t)$ is a constant $U$. Then the integral can be explicitly solved and the following closed form expression is obtained for the amount of money $x(t)$

$$\begin{array}{cl} x(t) &= M e^{it} + { U \over i } \left( ... ... + {U \over i} \right) e^{it} - { U \over i } . \end{array}$$

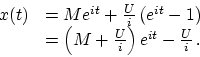
A regular continuously compounded deposit of $U$ per period is the equivalent of having an initial amount of money of $M + U/i$ with the additional adjustment of $U/i$ for the initial condition.

It is noted that the quantity $x(t)$ is an amount of money at the future time $t$, and is called the future value.

The last result above is one of the most basic formulas in finance. It can describe an annuity, an account from which money is drawn, or a mortage depending on whether $M$ and $U$ are chosen as positive or negative quantities. For example a mortgage situation occurs when $M < 0$ and $U > 0$.