
Back to Cfa research pages.
Examples of advanced versions of Cfa
We caution not to misinterpret these results. In some cases the results can change much depending on the numbers. We are not illustrating conclusions, but instead are illustrating techniques using our Cfa software. (Disclaimer)
There is quite a wide range of results on rent versus buy. The leveraging results depend very much on what the numbers are. This is one of the great powers and capabilities of Cfa: these sensitivies can be studied. The results on down payment are perhaps even more dramatic.
The calculations and results on this page were performed with the more advanced versions of Cfa. These more advanced versions allow single variables to be analyzed over a range of values, with corresponding results calculated and plotted. This is a very powerful analysis capability for graphical relationships and sensitivities to important variables can be studied.
Here is an example graph computed by Cfa of the first result shown below.
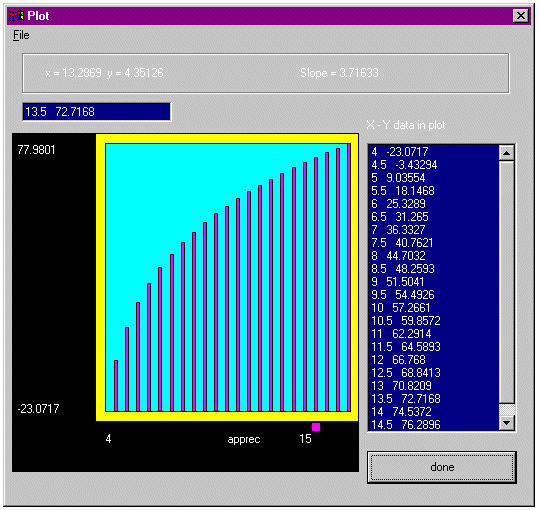
Calculation and graph of rate of return between
renting and buying as
a function of the apprecation rate of the home.
(Graph generated by more advanced versions of Cfa)
This graph is useful and portrays meaningful information. Moving the mouse over the data gives the data values as well as the slope (sensitivity). We admit though that higher quality graphics can be obtained by exporting this data into other tools designed specifically for graphics.
This graph is useful in the scientific sense because the data values themselves are displayed, and moving the mouse displays both the data values as well as the sensitivity. For example, at the point apprec = 5%, the sensitivity is about 21. This is the slope of the curve at this point. For every point the home appreciates (about this point), the rate of return goes up 21 points.
The "baseline" problem that we are working here uses the parameters for the problem discussed here. We will vary some of the parameters in this rent/buy problem, and we will portray the results graphically. (This graph is also shown above.)
..gvar percent-down 20.0 ..gvar home-cost 160000 ..gvar mortgage-interest 7.5 ..gvar extra-payments -200 ..gvar tax-bracket 25 ..gvar tax-bracket-differential 5 ..gvar apprec 5 ..gvar selling-percent 7.0 ..gvar rent-cost -650 ..gvar rent-inc 0.00 ..gvar account-rate 7 ..gvar additional-deposit 0
The rate of return on the difference between buying and renting depends most dramatically on the home appreciation rate, as this graph shows. This is an interesting result. We coined the word "leveraging curve" since it shows the leveraging effect of buying a home.
It may be hard to define what this rate of return on the difference between buying minus renting really means, and this is sometimes debated in textbooks. The PW may be a better measure for such a comparison, and this is discussed next.
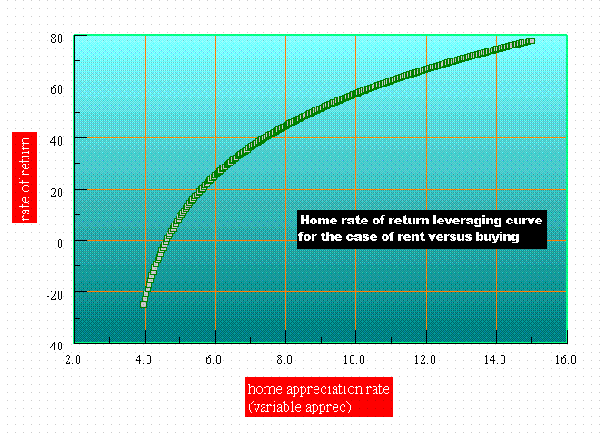
PW calculation Now we vary the apprec rate from 4 to 15 % and we compute the PW of the difference between buying and renting (buy - rent). The discount rate for the PW calculation is 6% yearly. (The per period rate is this number divided by 12.) This only takes a minute or two in Cfa and the data is (it is easy to export such data)
4.000000 -4316.187735 4.500000 -1831.882235 5.000000 714.018762 5.500000 3323.015932 6.000000 5996.645867 6.500000 8736.481918 7.000000 11544.135063 7.500000 14421.254784 8.000000 17369.529976 8.500000 20390.689870 9.000000 23486.504980 9.500000 26658.788069 10.000000 29909.395141 10.500000 33240.226451 11.000000 36653.227547 11.500000 40150.390322 12.000000 43733.754107 12.500000 47405.406772 13.000000 51167.485867 13.500000 55022.179780 14.000000 58971.728925 14.500000 63018.426955 15.000000 67164.622009
This is plotted below.

Plot of PW as a function of home appreciation rate
And of course, as we already know, we can do very well if the home appreciates at a high rate. The calculations here show this exact quantititative relationship, and can be performed in only a few minutes using the advanced versions of Cfa.
We use the same set of numbers as listed above, but this time we will vary the tax bracket from 15% to 45%. The calculated PW (discounted at 6%) on the difference between buying minus renting is given by this data:
15.000000 -1107.882959 16.000000 -925.692787 17.000000 -743.502615 18.000000 -561.312443 19.000000 -379.122270 20.000000 -196.932098 21.000000 -14.741926 22.000000 167.448246 23.000000 349.638418 24.000000 531.828590 25.000000 714.018762 26.000000 896.208934 27.000000 1078.399106 28.000000 1260.589278 29.000000 1442.779450 30.000000 1624.969622 31.000000 1807.159794 32.000000 1989.349966 33.000000 2171.540138 34.000000 2353.730310 35.000000 2535.920482 36.000000 2718.110654 37.000000 2900.300826 38.000000 3082.490998 39.000000 3264.681170 40.000000 3446.871342 41.000000 3629.061514 42.000000 3811.251686 43.000000 3993.441858 44.000000 4175.632030 45.000000 4357.822202
This data is plotted below.
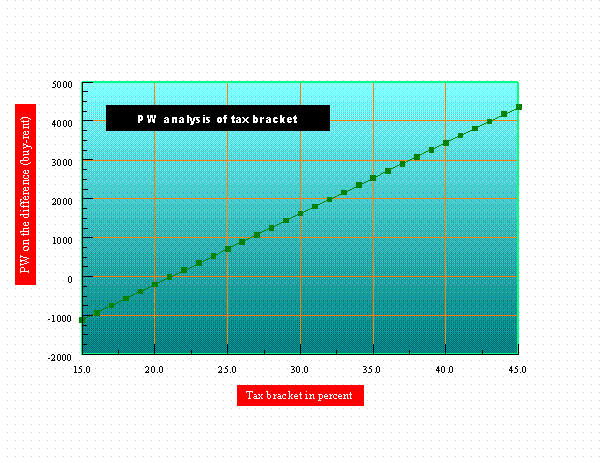
PW of buying minus renting as a function of tax bracket
This data is a straight line with a slope of 182.19. For every point that the tax bracket goes up, the PW (on the difference) goes up 182.19. Of course in the higher tax brackets we are better off buying because this increases the home mortgage interest deduction, and further we are worse off in the case of renting because we pay more tax in the interest earned on the CD. We have demonstrated the exact quantitative dependence on the tax bracket.
Also notice that there is a breakeven tax bracket (around 21%) where buying and renting will have about equal PW (when discounted at 6%). Of couse this breakeven value depends on what numbers we choose, and this is NOT a general conclusion. Cfa calculates the breakeven tax bracket to be 21.1% indeed, a very easy calculation.
We vary the percent down payment for the mortgage from 1% to 30% and we calculate both the PW and rate of return on the difference between buying minus renting. Again the results are very interesting.
PW. The PW (discounted at 6%) as a function of the percent down payment is computed as
1.000000 -511.154415 2.000000 -446.671617 3.000000 -382.188818 4.000000 -317.706019 5.000000 -253.223220 6.000000 -188.740421 7.000000 -124.257623 8.000000 -59.774824 9.000000 4.707975 10.000000 69.190774 11.000000 133.673573 12.000000 198.156371 13.000000 262.639170 14.000000 327.121969 15.000000 391.604768 16.000000 456.087567 17.000000 520.570365 18.000000 585.053164 19.000000 649.535963 20.000000 714.018762 21.000000 778.501561 22.000000 842.984359 23.000000 907.467158 24.000000 971.949957 25.000000 1036.432756 26.000000 1100.915554 27.000000 1165.398353 28.000000 1229.881152 29.000000 1294.363951 30.000000 1358.846750
This PW series of data is plotted below.
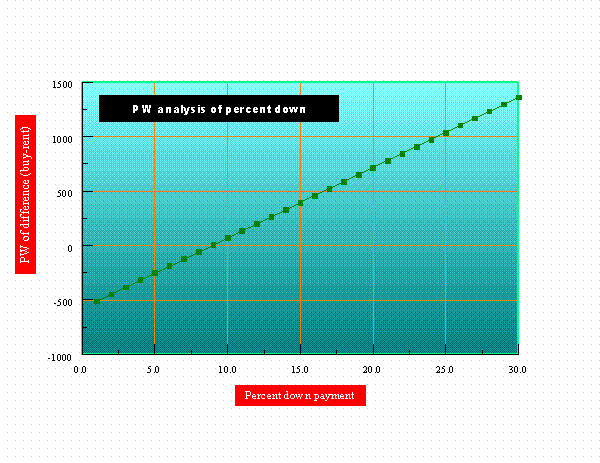
PW for buy-rent as a function of percent down payment
This is a straight line with slope 64.48. We note that the results on down payment can depend very much on what the numbers are. Try it with your own numbers.
Rate of return. Another interesting calculation is the rate of return on the difference as a function of the percent down payment. The data from this calculation is:
1.000000 5.007884 2.000000 5.107565 3.000000 5.213279 4.000000 5.325593 5.000000 5.445144 6.000000 5.572659 7.000000 5.708961 8.000000 5.854995 9.000000 6.011844 10.000000 6.180759 11.000000 6.363194 12.000000 6.560846 13.000000 6.775709 14.000000 7.010143 15.000000 7.266963 16.000000 7.549557 17.000000 7.862030 18.000000 8.209423 19.000000 8.597979 20.000000 9.035544 21.000000 9.532113 22.000000 10.100628 23.000000 10.758177 24.000000 11.527816 25.000000 12.441491 26.000000 13.544894 27.000000 14.906004 28.000000 16.631202 29.000000 18.898605 30.000000 22.036643
This data is plotted below.
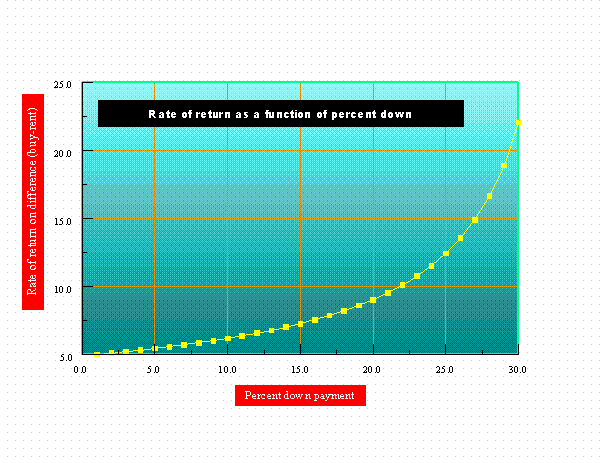
Rate of return on difference between buying minus renting as
a function of percent down
These results are very interesting.
HTML revision number: $Revision: 1.5 $