Picture of elementary version of Cfa
Back to Cfa research pages.
Download cash flow language template files used for the example on this page.
We will give a brief overview of the elementary version of Cfa while at the seme time providing some useful analysis for a buy versus rent problem. The elementary version of Cfa has many powerful features. It's a good deal.
We hope that you can benefit from the elementary version of this software. We also hope will will consider buying the relatively inexpensive expanded versions of Cfa, which have many additional features. These expanded features can make doing this kind of a problem much easier and much more fun, and more powerful kinds of analysis can be performed as well.
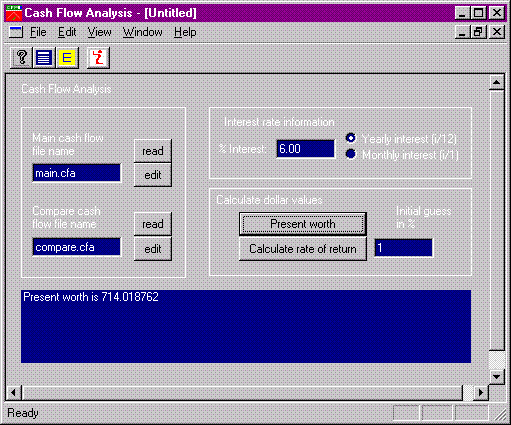
We show a picture of the elementary version of Cfa here.

Picture of elementary version of Cfa
This picture will aid us in our discussion.
Powerful, flexible, yet easy financial analysis tool. Cfa is a tool that allows investment micro-economics problems to be analyzed and solved easily. Cfa has features for specifying such problems, and Cfa has features for analyzing and solving such problems.
This is not rocket science. It is quite easy. See the simple example below. From the simple examples, more complex examples can be built.
Problems are specified using the cash flow language, which is a very simple computer programming language. The more advanced versions of Cfa allow these language specifications to be done visually, using the point-and-click visual editor. Of course notepad or any other editor can also be used to specify a cash flow problem.
Cash flow language specifications are usually very easy. Many things can be specified by a single line in a Cfa program. For example, the situation of paying 100 a month from months 0 to 60 can be easily described by a single line in a file. Another example of a one-line specification is a specification for a mortgage, or perhaps a CD, and there are several other items in the Cfa language. (These are described in detail in the book).
These specifications describe "what if" situations. What if I buy a home at ..., what if I rent and invest the money? How do I compare these, and so on...
Once a problem is specified, Cfa can also be used to analyze it and solve it. This is done by computing quantities such as the present worth (PW) or rate of return. Cfa also computes other intermediate results, such as the total cash flow series. The more advanced version of Cfa allow fancier quantities to be computed as well: such as breakeven values.
Powerful Language -- not a simple mortgage calculator. Cfa (and its more advanced versions) is a programming language that can describe both simple and complex investments. It is not merely a mortgage calculator, for it is capable of analyzing several simultaneous mortgages (say a second or third mortgage, or possibly one purely for investment). Very complex combinations of investments can be considered in one investment problem. Of course Cfa can do most of the traditional mortgage calculations, but it is much more powerful. In fact in the more advanced versions of Cfa this entire mortgage scenario can be defined in a file, and then this entire investment scenario would become a defined function that can be used as a single line within more complex investments. Maybe you wish to consider a mortgage combined with a life insurance investment, for example.
Comparisons. Cfa allows individual situations to be analyzed, or two situations can be compared. Comparing in many cases is like saying, "look item 1 costs x" and "item 2 costs y", and let me compute x and y, so that I can choose the cheapest. Here the x and y might be the cost of buying a home and the cost of renting, or it may be the cost of one mortgage with points versus another mortgage without points. Or you may be analyzing a series of perspective cash flows for a company or proposed investment you are making at your company. There are many, many such examples.
Cfa allows two files to be entered. This is how a problem, called a cash flow problem, is defined or described. These files defining the problem are called the main file and the compare file. If the compare file is not blank, then this second file describes the situation that we are comparing to. In our case, the main file describes buying, and the compare file describes renting. Of course, the main file and the compare files can be any files describing two cases we are trying to compare. For example, the main file could be one mortage with a certain number of points, and the compare file might be a second mortgage at a higher rate but with no points charges. There is an endless variety of such examples to compare.
The rest of the program is pretty obvious. There is a box to enter the discount rate and here this value is 6%. Roughly speaking, this is the "going rate for money". This rate is used to compute the present worth (PW), which is roughly how money is "added up" at the going rate. We think the basic features are obvious and we will not belabor these points, but instead will move onto a practical problem.
The examples below are slightly more complex, and before we give these more complex (and more powerful) examples, we wouuld first like to show how extremely easy Cfa can be. You don't have to use any variables, and you can just type in the numbers directly as shown in this example.
0 -160000.000000000000000 mortgage_loan 0 360 60 3 128000.000000000000000 7.5 25 const 0 60 1 -200 0.000000 60 205337.388560567370000 60 -14373.617199239718000 60 -11334.347140141843000
This file is called main1.cfa, and this is also included in the template kit.
The book provides many more examples of this sort, as well as more complex and increasingly more practical examples.
Each line in this file describes a cash flow item. The first line says, "pay 160000 at month 0". The second item says "take out a mortgage for 80% of the home value, use an interest rate of 7.5%, use a tax bracket of 25% for deductions for mortgage interest, make it a 30 year mortgage, but pay the balloon payment at month 60". The third line says pay 200 a month from months 0 to 60, to pay for miscellaneous home items, such as heating, insurance, etc. A few lines in a Cfa program as illustrated here can thus describe an extremely complex sitatuation. Further such complex situations can be described very quickly, by only entering a few lines.
Each line in a Cfa program is like an entire column in a spreadsheet. The example spreadsheet program for the above six lines is given below, with each line corresponding to a column.
| line 1 | line 2 | line 3 | line 4 | line 5 | line 6 |
| -160000 | 128000 | -200 | 0 | 0 | 0 |
| 0 | -694.995 | -200 | 0 | 0 | 0 |
| 0 | -695.143 | -200 | 0 | 0 | 0 |
| 0 | -695.292 | -200 | 0 | 0 | 0 |
| 0 | -695.443 | -200 | 0 | 0 | 0 |
| 0 | -695.594 | -200 | 0 | 0 | 0 |
| 0 | -695.746 | -200 | 0 | 0 | 0 |
| 0 | -695.899 | -200 | 0 | 0 | 0 |
| 0 | -696.053 | -200 | 0 | 0 | 0 |
| 0 | -696.208 | -200 | 0 | 0 | 0 |
| 0 | -696.364 | -200 | 0 | 0 | 0 |
| 0 | -696.521 | -200 | 0 | 0 | 0 |
| 0 | -696.679 | -200 | 0 | 0 | 0 |
| 0 | -696.838 | -200 | 0 | 0 | 0 |
| 0 | -696.998 | -200 | 0 | 0 | 0 |
| 0 | -697.159 | -200 | 0 | 0 | 0 |
| 0 | -697.321 | -200 | 0 | 0 | 0 |
| 0 | -697.484 | -200 | 0 | 0 | 0 |
| 0 | -697.648 | -200 | 0 | 0 | 0 |
| 0 | -697.813 | -200 | 0 | 0 | 0 |
| 0 | -697.979 | -200 | 0 | 0 | 0 |
| 0 | -698.146 | -200 | 0 | 0 | 0 |
| 0 | -698.314 | -200 | 0 | 0 | 0 |
| 0 | -698.484 | -200 | 0 | 0 | 0 |
| 0 | -698.654 | -200 | 0 | 0 | 0 |
| 0 | -698.825 | -200 | 0 | 0 | 0 |
| 0 | -698.997 | -200 | 0 | 0 | 0 |
| 0 | -699.171 | -200 | 0 | 0 | 0 |
| 0 | -699.345 | -200 | 0 | 0 | 0 |
| 0 | -699.521 | -200 | 0 | 0 | 0 |
| 0 | -699.698 | -200 | 0 | 0 | 0 |
| 0 | -699.876 | -200 | 0 | 0 | 0 |
| 0 | -700.054 | -200 | 0 | 0 | 0 |
| 0 | -700.235 | -200 | 0 | 0 | 0 |
| 0 | -700.416 | -200 | 0 | 0 | 0 |
| 0 | -700.598 | -200 | 0 | 0 | 0 |
| 0 | -700.781 | -200 | 0 | 0 | 0 |
| 0 | -700.966 | -200 | 0 | 0 | 0 |
| 0 | -701.152 | -200 | 0 | 0 | 0 |
| 0 | -701.339 | -200 | 0 | 0 | 0 |
| 0 | -701.527 | -200 | 0 | 0 | 0 |
| 0 | -701.716 | -200 | 0 | 0 | 0 |
| 0 | -701.907 | -200 | 0 | 0 | 0 |
| 0 | -702.098 | -200 | 0 | 0 | 0 |
| 0 | -702.291 | -200 | 0 | 0 | 0 |
| 0 | -702.485 | -200 | 0 | 0 | 0 |
| 0 | -702.68 | -200 | 0 | 0 | 0 |
| 0 | -702.877 | -200 | 0 | 0 | 0 |
| 0 | -703.074 | -200 | 0 | 0 | 0 |
| 0 | -703.273 | -200 | 0 | 0 | 0 |
| 0 | -703.473 | -200 | 0 | 0 | 0 |
| 0 | -703.675 | -200 | 0 | 0 | 0 |
| 0 | -703.878 | -200 | 0 | 0 | 0 |
| 0 | -704.082 | -200 | 0 | 0 | 0 |
| 0 | -704.287 | -200 | 0 | 0 | 0 |
| 0 | -704.493 | -200 | 0 | 0 | 0 |
| 0 | -704.701 | -200 | 0 | 0 | 0 |
| 0 | -704.91 | -200 | 0 | 0 | 0 |
| 0 | -705.121 | -200 | 0 | 0 | 0 |
| 0 | -705.332 | -200 | 0 | 0 | 0 |
| 0 | -121816 | -200 | 205337 | -14373.6 | -11334.3 |
If you read on, you will see that this describes our situation of buying a home. There is the payment of 160000, the mortgage/loan, the constant additional payments of 200 per month, and then the payments for selling costs and capital gain tax (approx). These payments are paid after the 5 year period (which is at month number 60). Also notice that we are assuming that we sell the house for 205337.38, which is entered as this amount at month number 60 (this represents a 5% yearly appreciation rate for the home). Of course you can change these numbers to be anything you like. Property taxes are included in the extra payments of 200 per month, or they can be included explicitly.
Thus in the simplest case you can use a calculator and just enter the numbers, as shown here. Of course Cfa can also be made to do simple kinds of arithmetic so you don't have to use a calculator.
Thus six lines of a very simple programming language can describe a practical mortgage/home-buying situation, including approximate tax effects. And an additional two lines in another file can describe the renting situation. Of course, Cfa is designed to be able to analyze much more complex situations also.
For the sake of completeness, the case of renting is also simply described by two lines in a Cfa program.
cd 0 60 1 32000.000000000000000 0 0.000000 0.583333333333333 30.000000000000000 const 0 60 1 -650 0.00
We list the spreadsheet equivalent of these two lines also, for sake of completeness. Again each line in the above description of renting corresponds to a column in spreadsheet. The negative amounts in line 1 are for the tax paid on the interest in the CD account.
| line 1 | line 2 |
| -32000 | -650 |
| -56 | -650 |
| -56.3267 | -650 |
| -56.6552 | -650 |
| -56.9857 | -650 |
| -57.3181 | -650 |
| -57.6525 | -650 |
| -57.9888 | -650 |
| -58.3271 | -650 |
| -58.6673 | -650 |
| -59.0095 | -650 |
| -59.3538 | -650 |
| -59.7 | -650 |
| -60.0482 | -650 |
| -60.3985 | -650 |
| -60.7509 | -650 |
| -61.1052 | -650 |
| -61.4617 | -650 |
| -61.8202 | -650 |
| -62.1808 | -650 |
| -62.5435 | -650 |
| -62.9084 | -650 |
| -63.2753 | -650 |
| -63.6445 | -650 |
| -64.0157 | -650 |
| -64.3891 | -650 |
| -64.7647 | -650 |
| -65.1425 | -650 |
| -65.5225 | -650 |
| -65.9047 | -650 |
| -66.2892 | -650 |
| -66.6759 | -650 |
| -67.0648 | -650 |
| -67.456 | -650 |
| -67.8495 | -650 |
| -68.2453 | -650 |
| -68.6434 | -650 |
| -69.0438 | -650 |
| -69.4466 | -650 |
| -69.8517 | -650 |
| -70.2592 | -650 |
| -70.669 | -650 |
| -71.0812 | -650 |
| -71.4959 | -650 |
| -71.9129 | -650 |
| -72.3324 | -650 |
| -72.7544 | -650 |
| -73.1788 | -650 |
| -73.6057 | -650 |
| -74.035 | -650 |
| -74.4669 | -650 |
| -74.9013 | -650 |
| -75.3382 | -650 |
| -75.7777 | -650 |
| -76.2197 | -650 |
| -76.6643 | -650 |
| -77.1115 | -650 |
| -77.5614 | -650 |
| -78.0138 | -650 |
| -78.4689 | -650 |
| 45285.1 | -650 |
These examples are discussed further below. We just wanted to show that it's really simple.
Now we will move on and add slightly more complexity to the situation. We will tackle the same problem as above, but now we will make it more general by using variables. This makes it much easier to change the problem, or to analyze the effect of some of the variables. We describe a situation of buying a sample home, and a situation of renting, as above. As shown below, the numbers describing the problem are described as the values of some variables, and it is easy to change these numbers to accomodate your personal situation.
Each situation is like a scenario and is described in a file. The buying case is in the file main.cfa and the comparison file or scenario (of renting) is described in the file compare.cfa.
The case of buying a home is described here. This is the main.cfa file.
Click here to download cash flow language template files used for the example on this page.
The comments in this cash flow program pretty much describe what we are doing. We note that we account for taxes paid (approximate) on the sale of the home. The "global" variables describe the problem, and we can also specify the differential tax bracket, which allows the tax bracket in the case of renting to be higher, since the mortgage deductions do not occur. These deductions are automatically made in the case of buying (approximately).
It's really pretty easy once you get the "knack" of it. That's the whole point of Cfa: to be able to do these kinds of analysis problems easily. And with our expanded versions of Cfa making these Cfa entries using the cash flow language is very easy, and is guided visually. That is, these files can be created by "point and click" and easily changed/modified/edited by "point and click."
Generally problems can thus be analyzed quickly and without lots of programming or setup. And when templates are supplied (where you can supply your own numbers), analyzing such problems can be very fast, and can take as little as only a few minutes.
OK, so here we go with the buying situation ...
..gvar percent-down 20.0 ..gvar home-cost 160000 ..gvar mortgage-interest 7.5 ..gvar extra-payments -200 ..gvar tax-bracket 25 ..gvar tax-bracket-differential 5 ..gvar apprec 5 ..gvar selling-percent 7.0 ..gvar rent-cost -650 ..gvar rent-inc 0.00 ..gvar account-rate 7 ..gvar additional-deposit 0 set down = < home-cost> * < percent-down> set down = < down> / 100.0 ..gvar downp < down> set x = < home-cost> * -1 0 < x> set mortgage = < home-cost> - < down> mortgage_loan 0 360 60 3 < mortgage> < mortgage-interest> < tax-bracket> const 0 60 1 < extra-payments> 0.000000 set x = < apprec> / 100. set x = < x> / 12.0 set x = < x> + 1 set factor = < x> ^ 60 set new-value = < factor> * < home-cost> 60 < new-value> set selling = < selling-percent> * < new-value> set selling = < selling> / -100. 60 < selling> set gain = < new-value> - < home-cost> set x = < gain> * < tax-bracket> set x = < x> / -100. 60 < x>
This case is simpler, and is described by the file shown below. This is the compare.cfa file, and describes the case we are comparing to.
In this case of renting, we take the money we would have used for a down payment, and we deposit it into a cd, paying tax on the interest. We account for the fact that the tax bracket is higher by 5% (this is only a guess) because mortgage deductions do not occur. The tax effects are only approximate. Then monthly rent payments are also made.
set tb = < tax-bracket> + < tax-bracket-differential> set x = < account-rate> / 12. cd 0 60 1 < downp> < additional-deposit> 0.000000 < x> < tb> const 0 60 1 < rent-cost> < rent-inc>
Cost of buying
Now that we have described the problem, we will give some results using Cfa. These results are computed using the elementary version of Cfa.
If we enter the name of the main file but leave the second file blank, we easily compute the present worth of the buying situation to be -35352.37. The negative number means that it is money paid out.
The cash flow series for the case of buying is computed, and placed into the file called main.dat. This file is shown here. The PW is the sum of the numbers in the second column when discounted at 6%.
0 -32200.000000 1 -894.994571 2 -895.143000 3 -895.292357 4 -895.442647 5 -895.593876 6 -895.746051 7 -895.899177 8 -896.053260 9 -896.208305 10 -896.364320 11 -896.521310 12 -896.679281 13 -896.838240 14 -896.998192 15 -897.159143 16 -897.321101 17 -897.484071 18 -897.648059 19 -897.813073 20 -897.979117 21 -898.146200 22 -898.314326 23 -898.483504 24 -898.653739 25 -898.825037 26 -898.997407 27 -899.170854 28 -899.345384 29 -899.521006 30 -899.697725 31 -899.875549 32 -900.054484 33 -900.234538 34 -900.415716 35 -900.598028 36 -900.781478 37 -900.966075 38 -901.151826 39 -901.338738 40 -901.526818 41 -901.716074 42 -901.906512 43 -902.098141 44 -902.290967 45 -902.484999 46 -902.680243 47 -902.876707 48 -903.074400 49 -903.273328 50 -903.473499 51 -903.674921 52 -903.877602 53 -904.081550 54 -904.286773 55 -904.493278 56 -904.701074 57 -904.910169 58 -905.120570 59 -905.332287 60 57613.560147
This says how much money we pay every month regarding the case of buying the house. It is interesting to examine these numbers. Note how much money we get back at the end. This data can be cut and pasted into a spreadsheet. Of course, the PW is the sum of the amount of money paid out, when discounted at 6%. Note that the deduction for mortgage interest is computed on a monthly basis, and is used to adjust the cash flow values.
There is another file computed called main.tmp which contains more useful information (we do not include it here), and it also contains a mortgage table.
Cost of renting
Now we repeat for the case of renting. If we enter the file compare.cfa as the first file, and leave the second file blank, then we very easily compute the PW to be -36066.39. This is the total cost of renting over the 5 year period.
The CD macro automatically accounts for tax paid on the CD interest, and is paid monthly according to the specified incremental tax bracket.
The cash flow series for renting is placed in the file main.dat, and we show this below.
0 -32650.000000 1 -706.000000 2 -706.326667 3 -706.655239 4 -706.985728 5 -707.318145 6 -707.652500 7 -707.988807 8 -708.327075 9 -708.667316 10 -709.009542 11 -709.353764 12 -709.699995 13 -710.048245 14 -710.398526 15 -710.750851 16 -711.105231 17 -711.461678 18 -711.820204 19 -712.180822 20 -712.543544 21 -712.908381 22 -713.275346 23 -713.644453 24 -714.015712 25 -714.389137 26 -714.764740 27 -715.142535 28 -715.522533 29 -715.904747 30 -716.289192 31 -716.675879 32 -717.064821 33 -717.456033 34 -717.849526 35 -718.245315 36 -718.643413 37 -719.043833 38 -719.446589 39 -719.851694 40 -720.259162 41 -720.669007 42 -721.081243 43 -721.495883 44 -721.912943 45 -722.332435 46 -722.754374 47 -723.178775 48 -723.605651 49 -724.035017 50 -724.466888 51 -724.901278 52 -725.338202 53 -725.777675 54 -726.219712 55 -726.664327 56 -727.111535 57 -727.561353 58 -728.013794 59 -728.468874 60 44635.081698
Also note that we get money back at the end of the 5 years.
Cost of buying minus cost of renting
And finally, we enter main.cfa as the main file and compare.cfa as the second file, so that we can compare buying to renting. The PW of this difference is computed to be 714.02. This says that buying minus renting is 714.02, and thus we are slightly better off in the case of buying.
Of course these results are all for the particular numbers we have chosen.
Double check
Generally it is not a good idea to blindly do a calculation without performing some kind of double check on the results. The check we provide here is for the ideal case when the mortgage and appreciation rates are both equal to 7.5% and the tax bracket is zero.
Thus change the numbers to those given here, and erase the compare.cfa renting file.
..gvar percent-down 20.0 ..gvar home-cost 160000 ..gvar mortgage-interest 7.5 ..gvar extra-payments -00 ..gvar tax-bracket 0 ..gvar tax-bracket-differential 5 ..gvar apprec 7.5 ..gvar selling-percent 0.0
Changing some numbers and recomputing a result is very easy with the elementary version of Cfa, and is even easier with the more powerful versions of Cfa.
We encourage you to try this analysis with higher home appreciation rates. A few more points on the home appreciation rate makes quite a dramatic difference in the results, as we hope you will soon discover.
The "news" just said that the home prices went up 13% last month (March 1998) for homes in the Oakland / San Francisco / San Jose / Silicon Valley Bay Area. Let's say that your home goes up 13% each year for five years, and we encourage you find for yourself what the rent versus buy results are.
With these numbers
..gvar percent-down 20.0 ..gvar home-cost 160000 ..gvar mortgage-interest 7.5 ..gvar extra-payments -200 ..gvar tax-bracket 25 ..gvar tax-bracket-differential 5 ..gvar apprec 13 ..gvar selling-percent 7.0
We quickly calculate the home buying situation (not even compared to renting, but as an absolute investment) to have a PW of $15000 and an (after tax) rate of return of 10.9%. These results are quite stunning!
If you own a home here you just made so much money that you can easily afford to buy our Cfa products.
This elementary version of Cfa has a number of additional features, and we cannot describe them all here.